casual卷积最初随WaveNet一起提出,WaveNet是一个生成模型，类似于早期的pixel RNN和Pixel CNN，主要用来生成语音，声音元素是一个点一个点生成的。WaveNet是利用卷积来学习t时刻之前的输入数据（音频），来预测t+1时刻的输出. 对输入数据的顺序很注重, t时刻的输出仅仅依赖于1,2,…,t-1时刻的输入，不会依赖于t+1时刻以及之后时刻的输入。这与BiLSTM的思想截然不同。
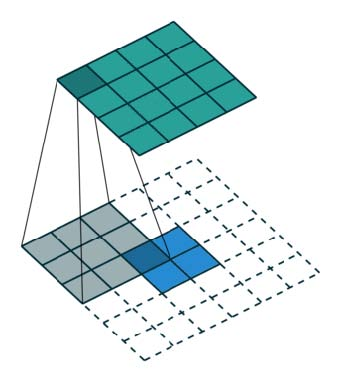
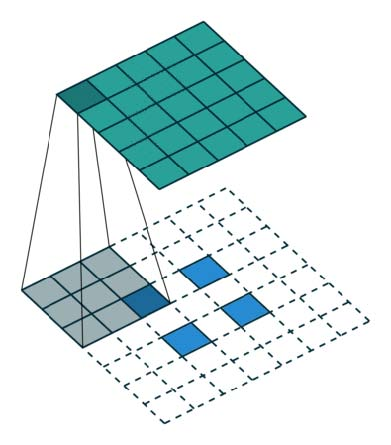
由于声音文件是时间上的一维数组，16KHz的采样率的文件，每秒钟就会有16000个元素，而上面所说的因果卷积的感受野非常小，即使堆叠很多层也只能使用到很少的数据来生成t时刻的的元素，为了扩大卷积的感受野，WaveNet采用了堆叠了（stack）多层扩张（dilated ）卷积(中篇里有提到)来增大网络的感受野，使得网络生成下一个元素的时候，能够使用更多之前的元素数值。1D扩张卷积如下图所示：
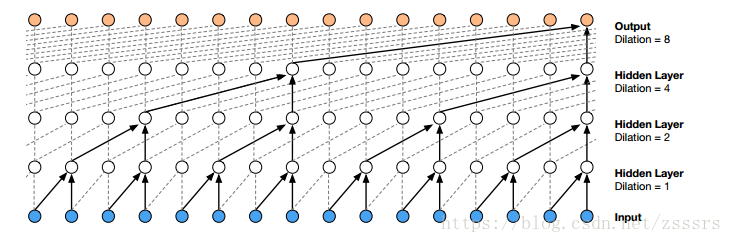
整个生成过程的动态图如下:
不知不觉又快到了找工作的季节，慕然回想一下自己这两年学过的知识，大部分都变得陌生却又有点熟悉。于是乎决定重拾自己之前在CSDN上写博客的热情，但是发现CSDN的界面又chou了许多… 所以还是花费了点时间自己搭Github Page + Hexo，准备把最近自己复习整理的知识点一一记录下来，与大家一起交流学习！ 话不多说，今天第一篇博客主要分享下卷积神经网络CNN中各种花式卷积操作，结合自己之前看过的论文和资料以及最近微博上爱可可老师分享的文章《A Comprehensive Introduction to Different Types of Convolutions in Deep Learning》,来一起感受下深度学习中“卷积”的魅力~ （注：本文主要翻译该篇文章，并加上自己的理解，同时会扩展提到其他几种不同的卷积形式）
本文内容较多，故分为上中下三篇，上篇包括：
中篇包括：
下篇为本人补充，包括：
对于许多应用程序和在许多网络架构中，我们经常希望进行与正常卷积相反方向的转换，即我们希望执行上采样。一些示例包括生成高分辨率图像并将低维特征映射到高维空间，例如自动编码器或语义分割。（在后面的示例中，语义分割首先在编码器中提取要素图，然后在解码器中恢复原始图像大小，以便它可以对原始图像中的每个像素进行分类。）
传统上，可以通过应用插值方案或手动创建规则来实现上采样。另一方面，诸如神经网络之类的现代架构倾向于让网络本身自动地学习正确的转换，而无需人为干预。为此，我们可以使用转置卷积。
转置卷积在文献中也称为反卷积或分数跨步卷积。然而，值得注意的是，“反卷积”这个名称不太合适，因为转置卷积不是信号/图像处理中定义的真实反卷积。从技术上讲，信号处理中的反卷积会逆转卷积运算。这里情况不同。因此，一些作者强烈反对将转置卷积称为反卷积。人们称它为反卷积主要是因为简单。稍后，我们将看到为什么将这种操作称为转置卷积是自然而且更合适的。
始终可以使用直接卷积实现转置卷积。对于下图中的示例，我们使用3 x 3内核在2 x 2输入上应用转置卷积，使用单位步幅填充2 x 2边框。上采样输出的大小为4 x 4。
有趣的是，通过应用花式填充和不同步幅，可以将相同的2 x 2输入图像映射到不同的图像大小。下面，转置卷积应用于相同的2 x 2输入（在输入之间插入1个0），使用单位步幅填充2 x 2边界的零。现在输出的大小为5 x 5。
在上面的例子中查看转置卷积可以帮助我们建立一些直觉。但是为了概括其应用，通过计算机中的矩阵乘法来研究它是如何实现的是有益的。从那里，我们也可以看到为什么“转置卷积”是一个合适的名称。
在卷积中，让我们定义C作为我们的内核，Large作为输入图像，Small作为来自卷积的输出图像。在卷积（矩阵乘法）之后，我们将大图像下采样为小的输出图像。矩阵乘法中的卷积的实现遵循C x Large = Small。
以下示例显示了此类操作的工作原理。它将输入Reshape为16 x 1矩阵，并将内核转换为稀疏矩阵（4 x 16）。然后在稀疏矩阵和有效输入之间应用矩阵乘法。之后，将得到的矩阵（4×1）转换回2×2输出。
现在，如果我们在方程的两边多重矩阵CT的转置，并使用矩阵与其转置矩阵的乘法给出单位矩阵的属性，那么我们有以下公式CT x Small = Large，如下所示下面的图片：
正如您在此处所看到的，我们执行从小图像到大图像的上采样。这就是我们想要实现的目标。现在，您还可以看到“转置卷积”这个名称的来源。